春雨里洗过的太阳

世间所有的相遇，都是久别重逢

数据结构与算法

发表于 更新于 分类于
本文字数： 3.2k 阅读时长 ≈ 3 分钟

一 数据结构

数据结构:是指相互之间存在一种或多种特定关系的数据元素的集合

数据结构=逻辑结构+数据的存储结构+(在存储结构上的)运算/操作

1.同一逻辑结构(唯一)对应多种存储结构(不唯一)

2.同样的运算在不同存储结构中实现不同(运算的实现依赖于存储结构)

1
2
3
4
5
6
7
8
9
10
11
12
逻辑结构大致分为: 
		1 线性结构
			线性表,栈,队列,数组等
		2 非线性结构
			树形结构
			图形结构
存储结构:
		1 顺序存储
		2 链式存储
		3 索引存储
		4 散列存储
数据的运算:增删查改

1 逻辑结构

1.1 线性表

​ 由0个或多个数据元素组成的有限序列.如果没有元素,称为空表,如果存在多个元素,则第一个元素无前驱,最后一个元素无后继,其他元素元素都有且只有一个前驱和后继(一对一)

1.2 非线性结构

​ 一个节点元素可能对应多个直接前驱和多个直接后继

如:树(一对多)和图(多对多)

2 存储结构

​ 数据的存储结构主要包括数据元素本身的存储和数据元素之间关系的表示,是数据的逻辑结构在计算中的表示

常见有顺序存储,连式存储,索引存储,和散列存储

2.1 顺序存储结构

​ 是把逻辑上相连的节点存储在物理位置相邻的存储单元上,节点间的逻辑关系由存储单元的邻接关系来体现

由此得到的存储结构是顺序存储结构,如数组;

​ 数据元素的存储对应于一块连续的存储空间,数据元素的前驱和后继通过数据元素在存储器的相对位置来反映

1
2
	 0  1  2
data a1 a2 a3 ...  连续的存储空间

优点:

节省空间,因为分配给数据的存储单元前部用来存储数据,节点间的关系没有占用额外的存储空间.(但从需要初始化长度来考虑,有可能有些存储节点没有存储数据造成空间的浪费),采用这种存储可实现对节点的存取,一个节点对应一个序号,可以根据序号直接计算节点的存储地址

缺点:

插入和删除元素需要移动元素,效率极低

2.1 链式存储结构

​ 数据元素的存储对应的是不连续的存储空间,每个存储节点对应一个需要存储的数据元素

每个节点由数据域和指针域组成,元素之间的逻辑关系通过存储节点间的连接关系反映出来

特点:

  1. 比顺序存储的密度要小(节点由指针和数据组成,所以相同空间内全存满顺序比链式存的多)
  2. 逻辑上相邻的节点物理上不必相邻
  3. 插入删除灵活(不必移动节点,只要改变节点中的指针)
  4. 查找节点是比顺序慢
1
head|头指针  ->  a1|a2的指针  -> a2|....  -> an|null

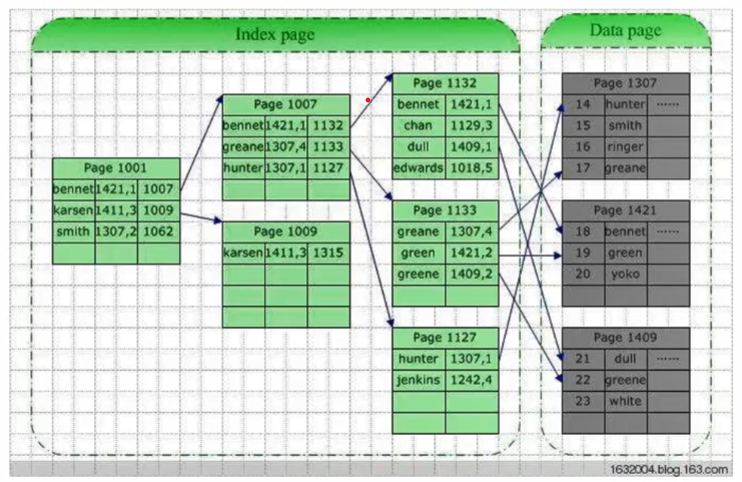
2.3索引存储结构

​ 除建立存储节点的信息外,还建立 附加的索引表来标识节点的地址

img

2.4 散列存储结构(hash存储)

根据节点的关键字直接计算该节点的存储地址

一种神奇的结构,添加查询速度都很快

二 算法与时间复杂度

1 算法

是指令的集合,是解决特定问题而规定的一系列操作

一个算法一般具有着五个特性:

1.输入,一个算法应以待解决的问题的信息为输入

2.输出:输入对应的指令后处理后的得到的信息

3.可行性

4.有穷性

5.确定性:对应于相同输入,结果应是一致的

2 算法优劣的依据:复杂度

时间复杂度和空间复杂度

时间频度:

一个算法执行所耗费的时间，从理论上是不能算出来的，必须上机运行测试才能知道。但我们不可能也没有必要对每个算法都上机测试，只需知道哪个算法花费的时间多，哪个算法花费的时间少就可以了。并且一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。

时间复杂度:

一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n),使得当n趋近于无穷大时，T（n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n)) 为算法的渐进时间复杂度，简称时间复杂度。在T(n)=4n²-2n+2中，就有f(n)=n²，使得T（n)/f(n)的极限值为4，那么O(f(n))，也就是时间复杂度为O(n²)

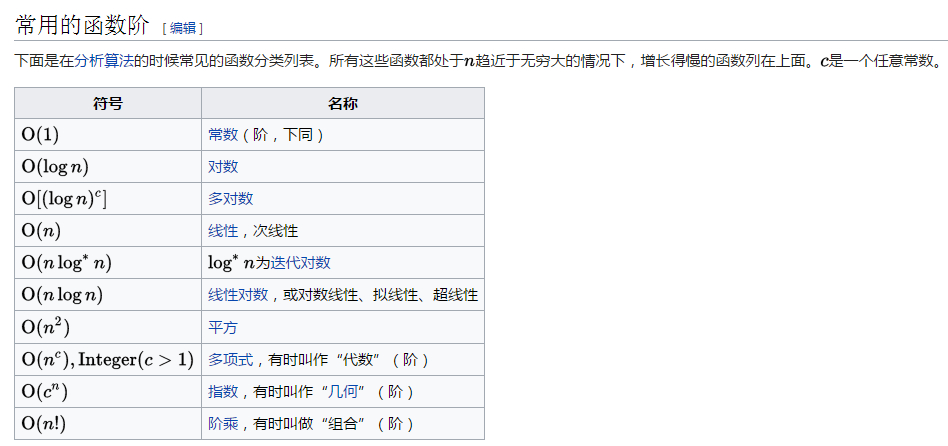
常用的函数阶:

img

一般讨论的都是最坏时间复杂度:

时间复杂度举例:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
1: o(1)
 Temp=i; i=j; j=temp;    
以上三条单个语句的频度均为1，该程序段的执行时间是一个与问题规模n无关的常数。算法的时间复杂度为常数阶，记作T(n)=O(1)。注意：如果算法的执行时间不随着问题规模n的增加而增长，即使算法中有上千条语句，其执行时间也不过是一个较大的常数。此类算法的时间复杂度是O(1)。
(2)、O(n2)

2.1. 交换i和j的内容

    sum=0；                 （一次）  
    for(i=1;i<=n;i++)     （n+1次）  
      for(j=1;j<=n;j++) （n2次）  
     sum++；            （n2次）  
解：因为Θ(2n2+n+1)=n2（Θ即：去低阶项，去掉常数项，去掉高阶项的常参得到），所以T(n)= =O(n2)；
2.2.

    for (i=1;i<n;i++)  
     {   
         y=y+1;         ①     
         for (j=0;j<=(2*n);j++)      
            x++;         ②        
     }      
解：
语句1的频度是n-1
语句2的频度是(n-1)*(2n+1)=2n2-n-1
f(n)=2n2-n-1+(n-1)=2n2-2；
又Θ(2n2-2)=n2
该程序的时间复杂度T(n)=O(n2).

一般情况下，对步进循环语句只需考虑循环体中语句的执行次数，忽略该语句中步长加1、终值判别、控制转移等成分，当有若干个循环语句时，算法的时间复杂度是由嵌套层数最多的循环语句中最内层语句的频度f(n)决定的。

(3)、O(n)

    a=0;  
    b=1;                      ①  
    for (i=1;i<=n;i++) ②  
    {    
     s=a+b;　　　　③  
     b=a;　　　　　④    
     a=s;　　　　　⑤  
    }  
解：
语句1的频度：2,
语句2的频度： n,
语句3的频度： n-1,
语句4的频度：n-1,
语句5的频度：n-1,
T(n)=2+n+3(n-1)=4n-1=O(n).

(4)、O(log2n)

    i=1;     ①  
    while (i<=n)  
    i=i*2; ②  
解：
语句1的频度是1,
设语句2的频度是f(n), 则：2^f(n)<=n;f(n)<=log2n
取最大值f(n)=log2n,
T(n)=O(log2n )

(5)、O(n3)

for(i=0;i<n;i++)  
   {    
      for(j=0;j<i;j++)    
      {  
         for(k=0;k<j;k++)  
            x=x+2;    
      }  
   }  
解：当i=m, j=k的时候,内层循环的次数为k当i=m时, j 可以取 0,1,...,m-1 , 所以这里最内循环共进行了0+1+...+m-1=(m-1)m/2次所以,i从0取到n, 则循环共进行了: 0+(1-1)*1/2+...+(n-1)n/2=n(n+1)(n-1)/6所以时间复杂度为O(n3).

空间复杂度:

空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度，记做S(n)=O(f(n))。比如直接插入排序的时间复杂度是O(n^2),空间复杂度是O(1) 。而一般的递归算法就要有O(n)的空间复杂度了，因为每次递归都要存储返回信息。一个算法的优劣主要从算法的执行时间和所需要占用的存储空间两个方面衡量。

（1）固定部分。这部分空间的大小与输入/输出的数据的个数多少、数值无关。主要包括指令空间（即代码空间）、数据空间（常量、简单变量）等所占的空间。这部分属于静态空间。
（2）可变空间，这部分空间的主要包括动态分配的空间，以及递归栈所需的空间等。这部分的空间大小与算法有关。
一个算法所需的存储空间用f(n)表示。S(n)=O(f(n))　　其中n为问题的规模，S(n)表示空间复杂度。