春雨里洗过的太阳

世间所有的相遇，都是久别重逢

线性表

发表于 更新于 分类于
本文字数： 11k 阅读时长 ≈ 10 分钟

线性表

1 简介

1:顺序表(java中的arrayList,vector就是) 2:单链表 3 双向链表(java中的linkedlist就是这个) 4 循环链表(循环单链,循环双链)

​ Java中的List我们经常会使用到，但是很少关注其内部实现，List是一个接口，里面定义了一些抽象的方法，其目的就是对线性表的抽象，其中的方法就是线性表的一些常用基本运算。 而对于线性表的不同存储结构其实现方式就有所不同了，比如ArrayList是对线性表顺序存储结构的实现，LinkedList是线性表链式存储结构的实现等。存储结构没有确定我们就不知道数据怎么存储，但是对于线性表这种逻辑结构中数据的基本操作我们可以预知，无非就是获取长度、获取指定位置的数据、插入数据、删除数据等等操作，可以参考List。

本文只对数据结构和一些常用算法学习，接下来的代码将选择性实现并分析算法。对线性表的抽象数据类型描述如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
 * autour : Fei
 * date : 2020/03/12 15:41
 * className : MyList
 * version : 1.0
 * description : 线性表的抽象数据类型
 */
public interface MyList {
    //返回线性表的大小,即数据元素的个数
    public int size();

    //返回线性表中序号为i的数据元素
    public Object get(int i);

    //判断线性表是否为空,空为true,否则为false
    public boolean isEmpty();

    //判断线性表是否包含数据元素e
    public boolean contains(Object e);

    //返回数据元素e在线性表中序号
    public int indexOf(Object e);

    //将数据元素e插入到线性表的i号位置
    public void add(int i,Object e);

    //将数据元素e插入到线性表末尾
    public void add(Object e);

    //将数据元素e插入到元素obj之前
    public boolean addBefore(Object obj,Object e);


    //将数据元素e插入到元素obj之后
    public boolean addAfter(Object obj,Object e);

    //删除线性表中序号为i的元素,并返回之
    public Object remove(int i);

    //删除线性表中第一个与e相同的元素
    public boolean remove(Object e);

    //替换线性表中序号为i的数据元素为e,返回原数据元素
    public Object replace(int i,Object e);
}

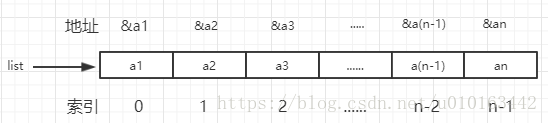
2 顺序存储结构

​ 把线性表中的所有元素按照其逻辑顺序依次存储在计算机存储器中指定存储位置开始的一块连续的存储空间中。在Java中创建一个数组对象就是分配了一块可供用户使用的连续的存储空间，该存储空间的起始位置就是由数组名表示的地址常量。线性表的顺序存储结构是利用数组来实现的。

img

在Java中，我们通常利用下面的方式来使用数组：

1
2
3
int[] array = new int[]{1,2,3}; //创建一个数组
Array.getInt(array, 0); //获取数组中序列为0的元素
Array.set(array, 0, 1); //设置序列为0的元素值为1

​ 这种方式创建的数组是固定长度的，其容量无法修改，当array被创建出来的时候，系统只为其分配3个存储空间，所以我们无法对其进行添加和删除操作。Array这个类里面提供了很多方法用于操作数组，这些方法都是静态的，所以Array是一个用于操作数组的工具类，这个类提供的方法只有两种：get和set，所以只能获取和设置数组中的元素，然后对于这两种操作，我们通常使用array[i]、array[i] = 0的简化方式，所以Array这个类用的比较少。

   另外一种数组ArrayList，其内部维护了一个数组，所以本质上也是数组，其操作都是对数组的操作，与上述数组不同的是，ArrayList是一种可变长度的数组。既然数组创建时就已经分配了存储空间，为什么ArrayList是长度可变的呢？长度可变意味着可以从数组中添加、删除元素，向ArrayList中添加数据时，实际上是创建了一个新的数组，将原数组中元素一个个复制到新数组后，将新元素添加进来。如果ArrayList仅仅做了这么简单的操作，那他就不应该出现了。ArrayList中的数组长度是大于等于其元素个数的，当执行add()操作时首先会检查数组长度是否够用，只有当数组长度不够用时才会创建新的数组，由于创建新数组意味着老数据的搬迁，所以这个机制也算是利用空间换取时间上的效率。但是如果添加操作并不是尾部添加，而是头部或者中间位置插入，也避免不了元素位置移动。

顺序表: 

1
2
3
4
5
6
7
8
9
10
1 根据索引查找元素的 时间复杂度: o(1)  1024 + index*4
2 根据具体的值查找 则时间复杂度为 0（n）
3 删除元素的 时间复杂度: o(n) 
删除第n个元素需要移动0个元素
删除第n-1个元素需要移动1个元素
删除第n-2个元素需要移动2个元素
''''
删除第1个元素需要移动n-1个元素
时间频度为: 0*1/n +1*1/n + 2*1/n  ... + (n-1)*1/n = (n-1)/2
时间复杂度为o(n)

2.1 基本运算的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
import java.util.Arrays;
/**
 * autour : Fei
 * date : 2020/03/12 15:41
 * className : MyList
 * version : 1.0
 * description : 线性表的抽象数据类型
 */
public class MyArrayList implements MyList {
    private Object[] elementData; //根据java.util.ArrayList,底层使用数组,元素为Object类型,没有确定长度
    private int size; //不是数组长度,而是元素的个数,默认为0

    /**
     * 有参构造
     * @param initialCapacity 指定数组的初始长度
     */
    public ArrayList(int initialCapacity) {
        //给数组elementData分配空间
        elementData = new Object[initialCapacity];
    }

    /**
     * 无参构造方法,调用有参方法,指定数组长度
     */
    public ArrayList(){
        this(4); //指定默认长度为4
        //不指定长度,长度为0
//      elementData = new Object[]{};
    }



    @Override
    public int size() {
        //返回数组元素个数
        return size;
    }

    @Override
    public Object get(int i) {
        //按索引返回数组的元素
        return elementData[i];
    }

    @Override
    public boolean isEmpty() {

        //size为0,则为true
        return size==0;
    }

    @Override
    public boolean contains(Object e) {
        //若果这个对象的索引在这个数组内,索引不为-1
        return indexOf(e) >= 0;
    }

    @Override
    public int indexOf(Object e) {
        //分为null和非null两种处理方式
        if(e == null){
            //遍历查找第一个为null的index
            for(int i =0;i<size;i++){
                if(elementData[i] == null){
                    return i;
                }
            }
        }else {
            //查找第一个等于
            for(int i=0;i<size;i++){
                if(elementData[i] == e){
                    return i;
                }
            }
        }
        //若没有找到,返回-1
        return -1;
    }

    @Override
    public void add(int i, Object e) {

        //添加时先判断数组是否满了,如果满了,就扩容
        if(elementData.length == size){
            grow();
        }
        //后移索引i和后边的元素,从最后一个开始
        for(int j=size;j>i;j--){ //j表示的索引是现有最大索引+1
            elementData[j] = elementData[j-1];
        }
        //将要添加的元素加进去
        elementData[i] = e;
        size++;
    }

    /**
     * 添加元素,并完成扩容操作
     * @param e
     */
    @Override
    public void add(Object e) {
//        //添加时先判断数组是否满了,如果满了,就扩容
//        if(elementData.length == size){
//            grow();
//        }
//        //给数组最后一个元素后边添加新元素,数组元素个数+1
//        elementData[size++] = e;
        this.add(size,e);
    }

    //扩容,将数组长度扩容到原来的3/2
    private void grow(){

//            //新创建一个新的数组,长度为旧数组的2倍
//            Object[] newArray = new Object[elementData.length*2];
//            //将旧数组的数据copy到新数组
//            for(int i =0;i<size;i++){ //有size个数据
//                newArray[i] = elementData[i];
//            }
//            //让elementData指向新数组
//            elementData = newArray;

        //使用Arrays的工具类实现,指定扩容的数组,新长度,和返回的指向
        elementData = Arrays.copyOf(elementData, elementData.length+elementData.length/2);
    }

    @Override
    public boolean addBefore(Object obj, Object e) {
        //获取obj的索引
        int index = this.indexOf(obj);
        //若数组没有此元素,添加失败
        if(index == -1){
            return false;
        }
        //进行添加操作
        this.add(index,e);
        return true;
    }

    @Override
    public boolean addAfter(Object obj, Object e) {
        //获取obj的索引
        int index = this.indexOf(obj);
        //若数组没有此元素,添加失败
        if(index == -1){
            return false;
        }
        //进行添加操作
        this.add(index+1,e);
        return true;
    }

    @Override
    public Object remove(int i) {
        Object o = elementData[i];
        //将索引i后边的元素前移即可,最后一个元素的索引为size-1
        for(int j=i;j<size-1;j++){
            //若j+1为最后一个元素,应为size-1,j为size-2
            elementData[j] = elementData[j+1];
        }
        elementData[size-1] = null;
        //返回被移除的那个对象
        return o;
    }

    @Override
    public boolean remove(Object e) {
        //判断数组是否包含此元素
        if(contains(e)){
            //删除此元素
            remove(indexOf(e));
            return true;
        }
        return false;
    }

    /**
     * 替换元素,返回被替换的元素
     * @param i
     * @param e
     * @return
     */
    @Override
    public Object replace(int i, Object e) {
        Object o = elementData[i];
        elementData[i]= e;
        return o;
    }


    /**
     * 打印集合中的数字,格式[123,3213,2323]
     * @return
     */
    @Override
    public String toString() {

        if(size == 0){
            return "[]";
        }
        StringBuilder stringBuilder = new StringBuilder("["); //字符串开始符号为[
        for(int i = 0 ;i<size;i++){
            if(i !=size-1){
                stringBuilder.append(elementData[i]+",");
            }else {
                stringBuilder.append(elementData[i]);
            }
        }
        stringBuilder.append("]"); //字符串结尾符号
        return stringBuilder.toString();
    }
}

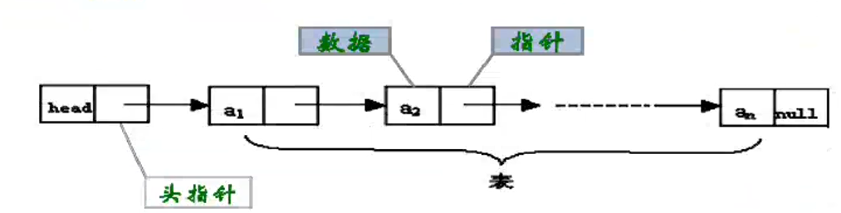
3链式存储结构-单链表

img

特点：

​ 数据元素存储的不是连续的存储空间，每个存储节点对应一个需要存储的元素每个节点是由数据域和指针域构成，元素间的关系通过存储节点间的链接关系反映出来，逻辑上相邻物理上不必相邻

缺点：

​ 1： 比顺序存储结构的密度的小，需要存储指针域

​ 2：查找节点比顺序结构慢（每个节点的地址不连续，无规律）

优点：

​ 1：插入，删除灵活，（不必移动节点，只需改变节点的指针，但需要先定位到元素）

​ 2：有元素才分配节点，不会有闲置节点

​ 3: 对比顺序存储结构，从存储指针域上浪费空间，从不浪费节点上来说节省空间*（无闲置节点）

单链表重要特性只能通过前驱节点找到后继节点，无法从后续查找前驱节点

尾结点的特点是next为空，单链表中通常用head表示首节点，由head的引用可以完成对整个链表的中所有的节点的访问

节点类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public class Node {

    //	private Object data;//要存储的数据
//	private  Node  next;
    Object data;//要存储的数据
    Node  next;
    public Node() {

    }
    public Node(Object data) {
        super();
        this.data = data;
    }
    public Node(Object data, Node next) {
        super();
        this.data = data;
        this.next = next;
    }
    public Object getData() {
        return data;
    }
    public void setData(Object data) {
        this.data = data;
    }
    public Node getNext() {
        return next;
    }
    public void setNext(Node next) {
        this.next = next;
    }
}

为了使程序更加简洁，通常在单链表的最前面添加一个元素，成为头结点，在头结点中不存储任何实质的元素，其next指向0号元素所在节点，这样可以对空表 ，费空表，以及首节点进行统一处理

img

img

模拟类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
public class MySingleChainedTable implements MyList {

    private Node head = new Node();//头结点，不存储数据，为了编程方便

    private int size;//一共有几个结点

    @Override
    public int size() {

        return size;
    }

    @Override
    public Object get(int i) {
        //可就和顺序表不一样了,不能通过索引直接计算定位，而需要从头结点开始进行查找
        Node p = head;
        for(int j = 0;j<=i;j++){
            p = p.next;
        }
        return p.data;
    }

    @Override
    public boolean isEmpty() {

        return size ==0;
    }

    @Override
    public boolean contains(Object e) {
        // TODO Auto-generated method stub
        return false;
    }

    @Override
    public int indexOf(Object e) {
        // TODO Auto-generated method stub
        return 0;
    }

    @Override
    public void add(int i, Object e) {
        //如果i位置错误报异常
        if(i <0  || i> size){
            throw new ArrayIndexOutOfBoundsException("数组指针越界异常："+i);
        }

        //找到前一个结点，从head结点开始
        Node p = head;
        for(int j = 0;j<i;j++){
            p = p.next;
        }
        //新创建一个结点
        //Node newNode = new Node(e);
        Node newNode = new Node();
        newNode.data = e;
        //newNode.next = null;
        //指明新结点的直接后继结点
        newNode.next = p.next;

        //指明新结点的直接前驱结点
        p.next = newNode;

        //size++
        size++;
    }

    @Override
    public void add(Object e) {
        this.add(size, e);

    }

    @Override
    public boolean addBefore(Object obj, Object e) {
        // TODO Auto-generated method stub
        return false;
    }

    @Override
    public boolean addAfter(Object obj, Object e) {
        // TODO Auto-generated method stub
        return false;
    }

    @Override
    public Object remove(int i) {
        // TODO Auto-generated method stub
        return null;
    }

    @Override
    public boolean remove(Object e) {
        // TODO Auto-generated method stub
        return false;
    }

    @Override
    public Object replace(int i, Object e) {
        // TODO Auto-generated method stub
        return null;
    }

    @Override
    public String toString() {
        if(size == 0){
            return "[]";
        }
        StringBuilder builder = new StringBuilder("[");
        Node p = head.next;
        for(int i=0;i<size;i++){
            if(i !=size -1){
                builder.append(p.data+",");
            }else{
                builder.append(p.data);
            }
            //移动指针到下一个结点
            p  = p.next;

        }
        builder.append("]");
        return builder.toString();
    }
}

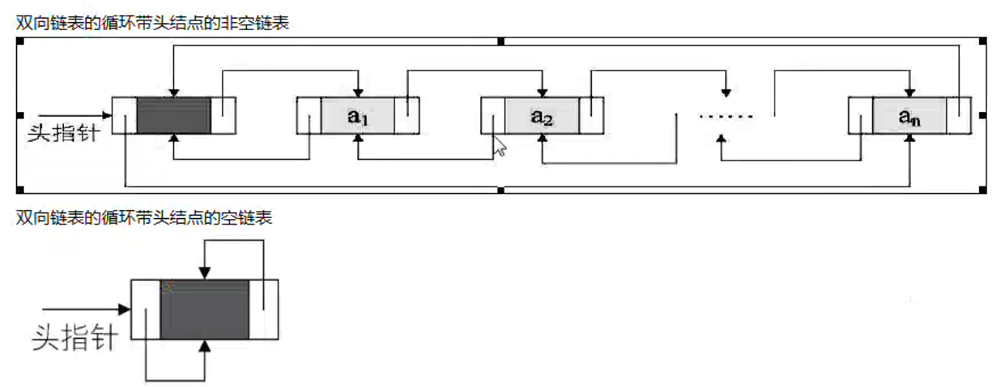
4 双向链表

单链表结构简单，缺点是只能通过节点的引用访问其后继节点，无法直接访问前驱结点，要在单链表中找到某个节点的前驱结点，必须从链表的首节点出发依次序向后寻找，需要o（n)时间 ，为此扩展单链表的 节点结构，使得通过节点的引用既可以访问前驱也可以访问后继，方法扩展指针域加一个域指向该节点的直接前驱

1
2
3
4
5
6
pre data next
pre 前驱指针域
data 数据
next 后继指针域
以此组合
null a next  <---> pre b next <---> ... <---> pre data null

与单链表同样的，为了使编程简洁，在双向链表中，加一个空的头结点和空的尾结点,这样不需要考虑链表由空变非空和由非空变空带来的head和tail问题，简化程序 ，Java中的linkedlist 就是双向链表

1
null null next  <---> pre a next .... <---> pre null null

实现….. 暂时没空

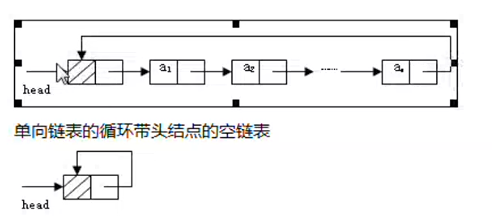
5 循环链表

循环链表就是无头无尾

循环链表中第一个节点就是最后一个节点，另外还有一种模拟循环链表的，就是在访问最后一个节点的时候手动跳转到第一个节点，，这样也可以实现循环链表，在直接使用循环链表比较麻烦或有问题时可以使用

单向循环链表

img

双向循环链表

img

实现、、、、暂时没空

6 操作受限的线性表–栈和队列

6.1 栈

又称堆栈，是运算受限的线性表

限制是仅允许在表的一段进行插入和删除操作，不允许在其他任何位置进行插入，查找，删除等操作

栈进行插入和删除的一段是栈顶，栈顶保存的元素称为栈顶元素，表的另一端为栈底，特性，后进栈的元素先出栈，又叫先进后出表

1
2
3
4
5
6
7
8
9
10
11
12
13
// 接口 push pop peek 常用词
public class Stack(){
  public int getSize();
    
  public boolean isEmpty();
  
  //元素入栈
  public void push(Object e);
  //栈顶元素出栈
  public Object pop();
  //去栈顶元素
  public Object peek();
}

存储结构

有两种：顺序存储结构和链式存储结构、

实现。。。。暂时没空

6.2 队列

也是一种运算受限的线性表，限制允许数据从表的一段进入，从另一端删除，插入元素为队尾，删除元素为队首，队尾插入元素为入队，删除元素为离队，即为先进先出表（FIFO)队尾（rear）队首front

1
2
3
4
5
6
7
8
9
10
11
12
//接口
public interface Queue{
    public int getSize();
    
  	public boolean isEmpty();
    //元素入队
  public void enqueue(Object e);
  //队首元素出队
  public Object dequeue();
  //去队首元素
  public Object peek();
}

存储结构：顺序存储结构和链式存储结构

顺序存储结构

1 使用数组的话

缺点：通过出队操作，front之前的空间不能再次得到，导致大量空间丢失，

解决使用循环数组作为存储结构

链式存储结构

基于删除元素方便，不会导致大量空间丢失

6.3 双端队列deque

两端都可以进行进队和出队

输出受限的双端队列： 两端都可以进，只有一段出

输入受限的双端队列： 两端都可以出，只有一端进

双端队列既可以做队列，亦可以做栈（只操作一端就是栈了）

1
2
3
4
5
6
7
8
9
10
java 中的栈和队列
栈：
	Stack（已过时）
队列：
	Queue（接口）
双端队列：
	Deque(栈操作建议使用)（接口）
	
linkedlist 实现了Queue和Queue 所以既可以做栈，队列也可以做线性表,底层是链表
ArrayDeque

使用：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
import java.util.Deque;
import java.util.LinkedList;

public class StackTest {

    public static void main(String[] args) {
        //使用栈做进制转换
        //给定一个十进制数
        int n = 100;

        //把十进制数转换成二进制
        int t = n;//被除数
        //String str = "";
        //定义一个空栈
        Deque stack  = new LinkedList();
        do{
            //除以2求余数
            int mod = t % 2;
            //输出余数
            //System.out.println(mod);
            //str =mod +str;
            //入栈
            stack.push(mod);
            //除以2得到商
            //int result = t / 2;
            //使用商做被除数
            //t = result;
            t = t /2 ;

        }while(t>0);//商>0

        //输出结果
        System.out.print(n+"------>");
        while(!stack.isEmpty()){//栈非空
            System.out.print(stack.pop());
        }
    }
}