树和二叉树

一树

一棵树（tree）是由n（n>0）个元素组成的有限集合，其中：

（1）每个元素称为结点（node）；

（2）有一个特定的结点，称为根结点或根（root）；

（3）除根结点外，其余结点被分成m（m>=0）个互不相交的有限集合，而每个子集又都是一棵树（称为原树的子树）

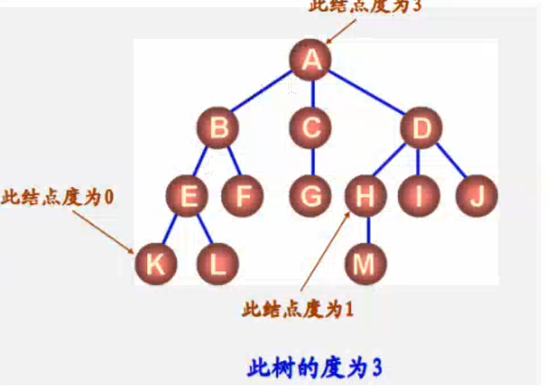
1.1 节点的度和树的度

树的度——也即是宽度，简单地说，就是结点的分支数。以组成该树各结点中最大的度作为该树的度，树中度为零的结点称为叶结点或终端结点。树中度不为零的结点称为分枝结点或非终端结点。除根结点外的分枝结点统称为内部结点

节点的度——节点拥有子树的树目为节点的度

1.2 节点的层次和树的深度

节点的层次从根开始定义，层次为1 的节点为根节点，其子树的根的层次为2，树中节点的最大层次数称为树的深度或高度

1.3 节点间的关系

对于一棵子树中的任意两个不同的结点，如果从一个结点出发，按层次自上而下沿着一个个树枝能到达另一结点，称它们之间存在着一条路径。可用路径所经过的结点序列表示路径，路径的长度等于路径上的结点个数减1.

父亲，儿子，兄弟
	节点的直接前驱为父节点
 	节点的直接后继为子节点
  	同一个父节点的其他节点为兄弟
祖先，子孙，堂兄弟
 	将父子关系扩展得到，祖先，子孙，堂兄弟关系
 	节点的祖先是从根到该节点路径上的所有节点
	以某节点为根的树中的任意节点为该节点的子孙
	父亲在同一层的节点为堂兄弟

1.4 有序树，m叉树，森林

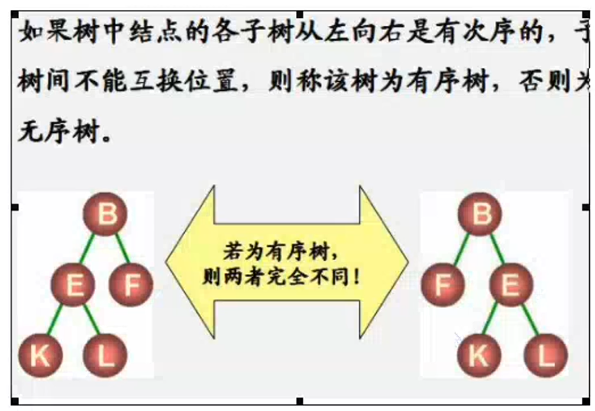
如果将树中的节点的各子树看成是从左到右是由次序的，称该树为有序树，若不考虑子树的顺序则为无序树

对于有序树，我们可以明确定义每个节点的第一个孩子，第二个孩子等，只到最后一个，若不特别指明，一般讨论的树都是有序树

树中所有节点的最大度数为m的有序树为m叉树

森林

指若干棵互不相交的树的集合

树和森林概念相近，删去树的根节点即为森林，森林加上根节点即为树

二二叉树

每个节点的度都不超过2的树为2叉树，，每个节点只有0，1，2个节点，每个孩子都有左右之分

二叉树是n个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成，是有序树。当集合为空时，称该二叉树为空二叉树。在二叉树中，一个元素也称作一个节点

二叉树是递归定义的，其节点有左右子树之分，逻辑上二叉树有五种基本形态：

1、空二叉树

2、只有一个根节点的二叉树

3、只有左子树

4、只有右子树

5 完全二叉树（在一棵满二叉树中，在最下层从最右侧起去掉相邻的若干叶子节点，得到的二叉树为完全二叉树）

6 满二叉树（每一层都是最多的节点）

满二叉一定位完全二叉树，完全二叉不一定是满二叉树

二叉树的性质

1 第i层上最多有2的i-1次方个节点（跟为第一层）
2：高度为h的二叉树最多有2的h次方-1个节点
3：终端节点数为n0 ,度为2 的节点数为n2,则n0 = n2 +1
4: 有n个节点的完全二叉树的高度为【log2N】+1 【log2N】向下取整（以2位低n的对数）
5：含有n>=1个节点的高度之多为n-1,高度至少为【log2N】+1 【log2N】向下取整
6：若对一棵有n个节点的完全二叉树进行顺序编号（1≤i≤n），那么，对于编号为i（i≥1）的节点：
当i=1时，该节点为根，它无双亲节点  。
当i>1时，该节点的双亲节点的编号为i/2  。
若2i≤n，则有编号为2i的左节点，否则没有左节点 。
若2i+1≤n，则有编号为2i+1的右节点，否则没有右节点

存储结构

顺序存储和链式存储，实际中链式用的最多

顺序存储结构存储满二叉树和完全二叉树非常合适高效，但其他的树会造成空间浪费（必须用虚节点将二叉树补全为完全二叉树来存储，会造成空间浪费）

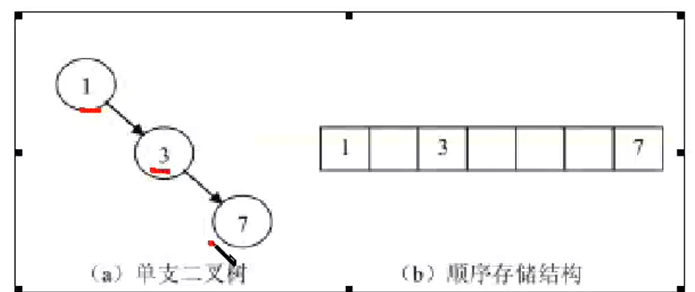
链式存储结构

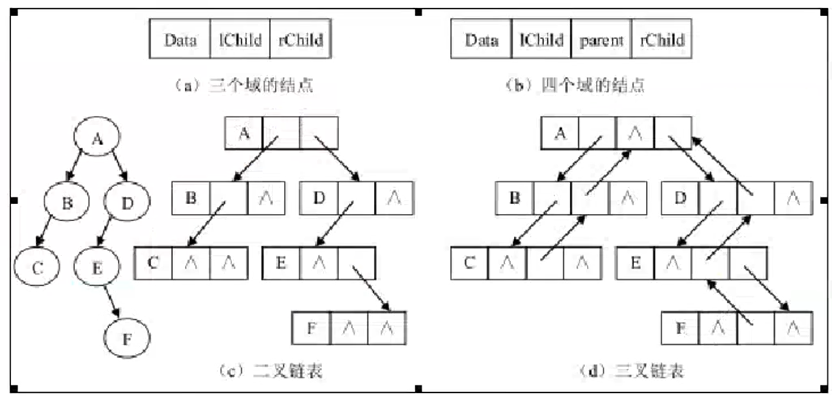
三二叉树的遍历

简单来说就是人为的将非线性结构线性化

遍历类型：先左后右

DLR: 先序遍历（根节点，左节点，右节点）可用递归，若不用则遍历需要用栈
LDR: 中序遍历（左节点，根节点，右节点）可用递归，若不用则遍历需要用栈
LDR: 中序遍历
LRD: 后序遍历（左节点，右节点，根节点）可用递归，若不用则遍历需要用栈
层次遍历：不可用递归，借助队列可以实现

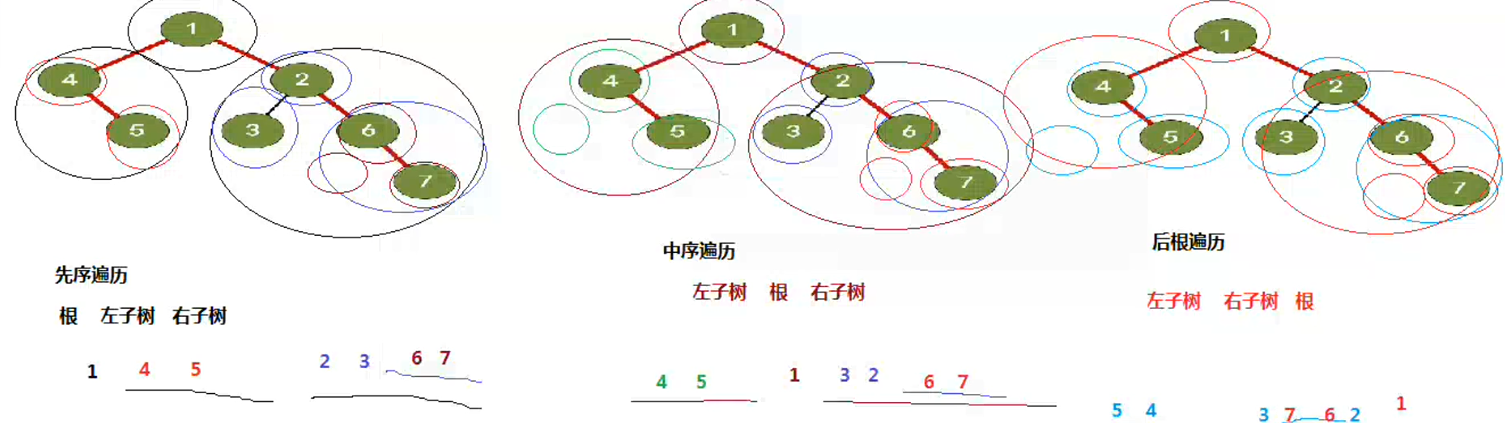
特性：

给你一个中序遍历的，再给你一个左或右，可以逆推出 右或左，但根据左右推不出中序
中序：4 5 1 3 2 6 7
后序：5 4 3 7 6 2 1
推出先序为：1 4 5 2 3 6 7

节点类：

/**
 * 二叉链表的结点
 * @author Administrator
 *
 */
public class Node {
	Object value; //结点值
	Node leftChild;//左子树的引用
	Node rightChild;//右子树的引用
	public Node(Object value) {
		super();
		this.value = value;
	}

	public Node(Object value, Node leftChild, Node rightChild) {
		super();
		this.value = value;
		this.leftChild = leftChild;
		this.rightChild = rightChild;
	}
	@Override
	public String toString() {
		return "Node [value=" + value + ", leftChild=" + leftChild
				+ ", rightChild=" + rightChild + "]";
	}
}

二叉树实现接口：

/**
 * 二叉树接口
 * 可以有不同的实现类，每个类可以使用不同的存储结构，比如顺序结构、链式结构
 * @author Administrator
 *
 */
public interface BinaryTree {
	/**
	 * 是否空树
	 * @return
	 */
	public boolean isEmpty();
	/**
	 * 树结点数量
	 * @return
	 */
	public int size();
	
	/**
	 * 获取二叉树的高度
	 * @return
	 */
	public int getHeight();
	/**
	 * 查询指定值的结点
	 * @param value
	 * @return
	 */
	public Node findKey(int value); // 查找
	/**
	 * 前序递归遍历
	 */
	public void preOrderTraverse(); 
	/**
	 * 中序遍历递归操作
	 */
	public void inOrderTraverse();  	
	/**
	 * 后序遍历递归操作
	 */
	public  void postOrderTraverse();
	/**
	 * 后序遍历递归操作
	 * @param node  树根结点
	 */
	public  void postOrderTraverse(Node node); 
	/**
	 * 中序遍历非递归操作
	 * 1）对于任意节点current，若该节点不为空则将该节点压栈，并将左子树节点置为current，重复此操作，直到current为空。 
	 * 2）若左子树为空，栈顶节点出栈，访问节点后将该节点的右子树置为current
	 * 3) 重复1、2步操作，直到current为空且栈内节点为空。 
	 */
	public void inOrderByStack();
	/**
	 *   前序遍历非递归操作
	 *   1）对于任意节点current，若该节点不为空则访问该节点后再将节点压栈，并将左子树节点置为current，重复此操作，直到current为空。 
	 *   2）若左子树为空，栈顶节点出栈，将该节点的右子树置为current 
	 *   3) 重复1、2步操作，直到current为空且栈内节点为空。
	 */
	public  void preOrderByStack(); 
	/**
	 * 后序遍历非递归操作
	 * 1）对于任意节点current，若该节点不为空则访问该节点后再将节点压栈，并将左子树节点置为current，重复此操作，直到current为空。 
	 * 2）若左子树为空，取栈顶节点的右子树，如果右子树为空或右子树刚访问过，则访问该节点，并将preNode置为该节点 
	 * 3) 重复1、2步操作，直到current为空且栈内节点为空。 
	 */
	public  void postOrderByStack(); 
	
	/**
	 * 按照层次遍历二叉树
	 */
	public void levelOrderByStack();
}

实现：

package com.bjsxt.datastructure.btree;

import java.util.Deque;
import java.util.LinkedList;
import java.util.Queue;

public class LinkedBinaryTree implements BinaryTree{
	private Node root;//根结点
	//private int size;
	
	public LinkedBinaryTree() {
		super();
	}

	public LinkedBinaryTree(Node root) {
		super();
		this.root = root;
	}

	@Override
	public boolean isEmpty() {		
		return root == null;
	}

	@Override
	public int size() {
		System.out.println("二叉树结点个数：");
		return this.size(root);
	}
	private int size(Node root) {
		if(root == null){
			return 0;
		}else{			
			//获取左子树的size
			int nl = this.size(root.leftChild);
			//获取右子树的size
			int nr = this.size(root.rightChild);			
			//返回左子树、右子树size之和并加1
			return nl+nr+1;
		}
	}

	@Override
	public int getHeight() {
		System.out.println("二叉树的高度是：");
		return this.getHeight(root);
	}
	
	private int getHeight(Node root){
		if(root == null){
			return 0;
		}else{			
			//获取左子树的高度
			int nl = this.getHeight(root.leftChild);
			//获取右子树的高度
			int nr = this.getHeight(root.rightChild);			
			//返回左子树、右子树较大高度并加1
			return nl > nr ? nl+1:nr+1;
		}
	}

	@Override
	public Node findKey(int value) {
		
		return this.findKey(value, root);
	}
	
	public Node findKey(Object value,Node root) {
		
		if(root == null){//递归结束条件1：结点为空，可能是整个树的根节点，也可能是递归调用中叶子节点中左孩子和右孩子
			return null;
		}else if(root != null && root.value == value){//递归的结束条件2：找到了
			return root;
		}else {//递归体
			Node node1 = this.findKey(value, root.leftChild);
			Node node2 = this.findKey(value, root.rightChild);
			if(node1 != null && node1.value == value){
				return node1;
			}else if(node2 != null && node2.value == value){
				return node2;
			}else{
				return null;
			}
		}
		
	} 
	
	@Override
	public void preOrderTraverse() {		
		if(root != null){
			//1.输出根结点的值
			System.out.print(root.value+"  ");
			//2.对左子树进行先序遍历
			//构建一个二叉树，根是左子树的根
			BinaryTree  leftTree = new LinkedBinaryTree(root.leftChild);
			leftTree.preOrderTraverse();
			//对右子树进行先序遍历
			//3.构建一个二叉树，根是左子树的根
			BinaryTree  rightTree = new LinkedBinaryTree(root.rightChild);
			rightTree.preOrderTraverse();
		}		
	
	}

	@Override
	public void inOrderTraverse() {
		System.out.println("中序遍历");
		this.inOrderTraverse(root);
		System.out.println();
		
	}
	
	private void inOrderTraverse(Node root) {//node7
		if(root != null){
			//遍历左子树
			this.inOrderTraverse(root.leftChild);//null
			//输出根的值
			System.out.print(root.value+"  ");//7
			//遍历右子树
			this.inOrderTraverse(root.rightChild);//null
		}		
	}

	@Override
	public void postOrderTraverse() {
		System.out.println("后序遍历");
		this.postOrderTraverse(root);
		System.out.println();
		
	}

	@Override
	public void postOrderTraverse(Node node) {
		if(node != null){
			//遍历左子树
			this.postOrderTraverse(node.leftChild);
			//遍历右子树
			this.postOrderTraverse(node.rightChild);
			//输出根的值
			System.out.print(node.value+"  ");
		}
		
	}

	@Override
	public void inOrderByStack() {
		System.out.println("中序非递归遍历:");
		// 创建栈
		Deque<Node> stack = new LinkedList<Node>();
		Node current = root;
		while (current != null || !stack.isEmpty()) {
			while (current != null) {
				stack.push(current);
				current = current.leftChild;
			}

			if (!stack.isEmpty()) {
				current = stack.pop();
				System.out.print(current.value + " ");
				current = current.rightChild;
			}
		}
		System.out.println();	
		
	}

	@Override
	public void preOrderByStack() {
		// TODO Auto-generated method stub
		
	}

	@Override
	public void postOrderByStack() {
		// TODO Auto-generated method stub
		
	}

	@Override
	public void levelOrderByStack() {
		System.out.println("按照层次遍历二叉树");
		if(root == null) return;
	    Queue<Node> queue = new LinkedList<Node>() ;
	    queue.add(root);
	    while(queue.size() != 0)
	    {
	        int len = queue.size();
	        for(int i=0;i <len; i++)
	        {
	        	Node temp = queue.poll();
	            System.out.print(temp.value+" ");
	            if(temp.leftChild != null)  queue.add(temp.leftChild);
	            if(temp.rightChild != null) queue.add(temp.rightChild);
	        }
	    }
	    
	    System.out.println();
		
	}

}

测试类：

package com.bjsxt.datastructure.btree;

public class Test {

	public static void main(String[] args) {
		//创建一个二叉树
		Node node5 = new Node(5, null, null);
		Node node4 = new Node(4, null, node5);
		Node node3 = new Node(3, null, null);
		Node node7 = new Node(7, null, null);
		Node node6 = new Node(6, null, node7);
		
		Node node2 = new Node(2, node3, node6);
		
		Node node1 = new Node(1,node4,node2);
		
		BinaryTree  btree = new LinkedBinaryTree(node1);
		//BinaryTree  btree = new LinkedBinaryTree();
		
		//判断二叉树是否为空
		System.out.println(btree.isEmpty());
		
		//先序遍历递归  1  4  5  2  3  6  7
		System.out.println("先序遍历");
		btree.preOrderTraverse();
		System.out.println();
		
		//中序遍历递归  4  5  1  3  2  6  7
		btree.inOrderTraverse();
		
		//后序遍历递归  5  4  3  7  6  2  1 
		btree.postOrderTraverse();
		
		
		//中序遍历非递归（借助栈） 4  5  1  3  2  6  7
		btree.inOrderByStack();
		
		//按照层次遍历（借助队列）  1  4  2  5  3  6  7
		btree.levelOrderByStack();
		//在二叉树中查找某个值
		System.out.println(btree.findKey(1));
		
		//二叉树的高度
		System.out.println(btree.getHeight());
		
		//二叉树的结点数量
		System.out.println(btree.size());
	}
}

四二叉搜索树

二叉排序树（Binary Sort Tree），又称二叉查找树（Binary Search Tree），亦称二叉搜索树。是数据结构中的一类。在一般情况下，查询效率比链表结构要高。

一棵空树，或者是具有下列性质的二叉树：

（1）若左子树不空，则左子树上所有结点的值均小于它的根结点]的值；

（2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；

（3）左、右子树也分别为二叉排序树；

【注】：以上的三种定义在不同的数据结构教材中均有不同的定义方式但是都是正确的在开发时需要根据不同的需求进行选择

【注2】：没有键值相等的结点。

五平衡二叉树

自平衡二叉查找树，又称AVL树

它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树，平衡二叉树一定时二叉搜素树，反之不一定

平衡因子：节点的平衡因子是节点的左子树的高度减去右子树的高度

平衡二叉树：每个节点的平衡因子都为1，-1，0，的二叉排序树，

平衡二叉树的目的是减少二叉查找树的层次，提高查找速度。

实现方法：

1	AVL ,红黑树，替罪羊树，Treap，伸展树等

六红黑树

R-B Tree ，是一种平衡二叉树，红黑树的每个节点上都有存储为表示节点的颜色，可以为红或黑

红黑树的特性：

1：每个节点为黑色或红色

2：根节点为黑色

3：每个叶子节点（nil）为黑色（这里的叶子节点是指为空的叶子节点）

4：如果一个节点为红色，则他的子节点必须为黑色

5：从一个节点到该节点的子孙节点的所有路径包含相同树目的黑节点

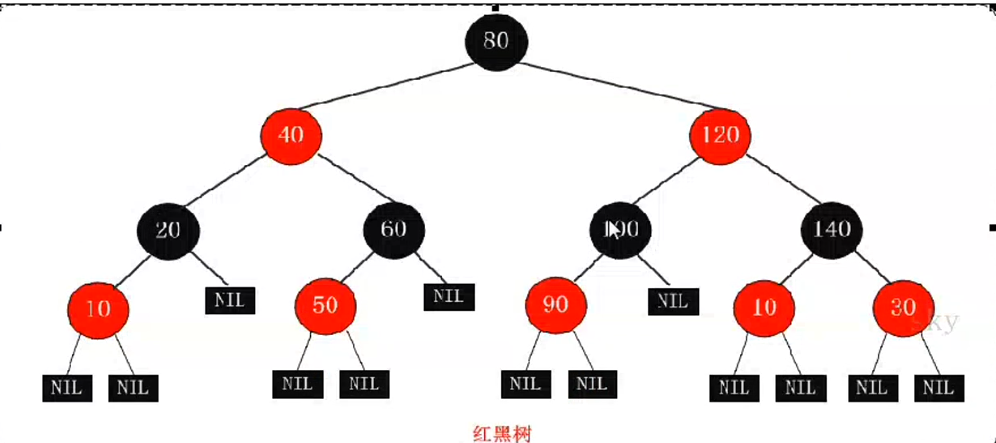
主要用来存储有序的数据，时间复杂度为o(logn),效率高

可以在o(logn)内做查找，插入和删除，例如java中的treeset和treemap，linux的内存管理都是通过红黑树实现的

七 b树（balanced tree）

与平衡二叉树相比是多叉的，可以降低树的高度，提高查找效率

b树应文件系统的要求而发展起来，如读取硬盘的数据

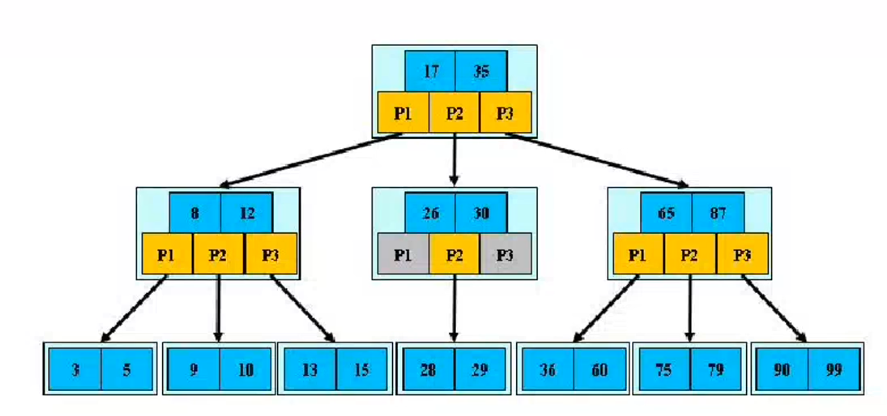
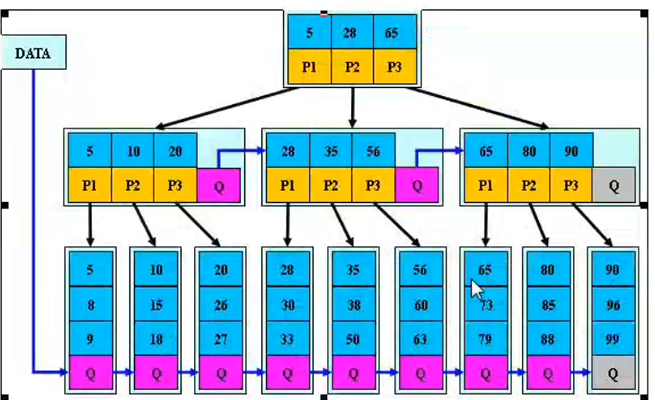
八 b+树

在b-树的基础上，为叶子节点增加链表指针，所有的关键字都在叶子节点中出现，非叶子节点作为叶子节点的索引，b+树总是到叶子节点才命中

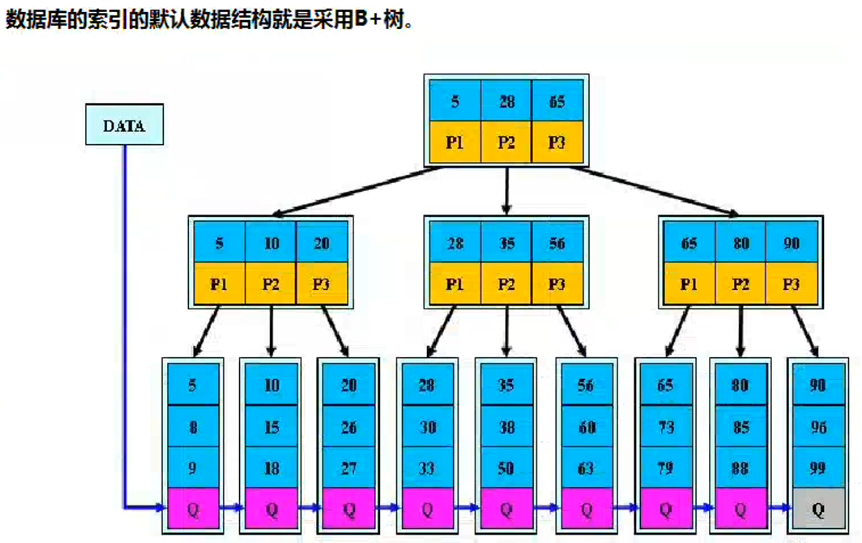
九 b*树

B*树是B+树的变体，区别在于它把非叶子节点的数据也用链表串起来，非跟和非叶子节点在增加指向兄弟的指针

一 树