一 图的定义
多对多的关系,是一种网状数据结构。图由非空的顶点集合和一个描述顶点之间关系的集合组成
1.顶点(vertex):图中的数据元素,如图一。
2.边(edge):图中连接这些顶点的线,如图一。
所有的顶点构成一个顶点集合,所有的边构成边的集合,一个完整的图结构就是由顶点集合和边集合组成。图结构在数学上记为以下形式:
G=(V,E) 或者 G=(V(G),E(G))
其中 V(G)表示图结构所有顶点的集合,顶点可以用不同的数字或者字母来表示。E(G)是图结构中所有边的集合,每条边由所连接的两个顶点来表示。
图结构中顶点集合V(G)不能为空,必须包含一个顶点,而图结构边集合可以为空,表示没有边。
1.无向图(undirected graph)
如果一个图结构中,所有的边都没有方向性,那么这种图便称为无向图。典型的无向图,如图二所示。由于无向图中的边没有方向性,这样我们在表示边的时候对两个顶点的顺序没有要求。例如顶点VI和顶点V5之间的边,可以表示为(V2, V6),也可以表示为(V6,V2)。
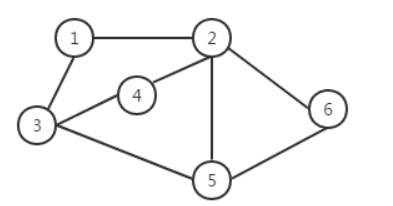
对于上图无向图,对应的顶点集合和边集合如下:
V(G)= {V1,V2,V3,V4,V5,V6}
E(G)= {(V1,V2),(V1,V3),(V2,V6),(V2,V5),(V2,V4),(V4,V3),(V3,V5),(V5,V6)}
2.有向图(directed graph)
一个图结构中,边是有方向性的,那么这种图就称为有向图,如图三所示。由于图的边有方向性,我们在表示边的时候对两个顶点的顺序就有要求。我们采用尖括号表示有向边,例如<V2,V6>表示从顶点V2到顶点V6,而<V6,V2>表示顶点V6到顶点V2。
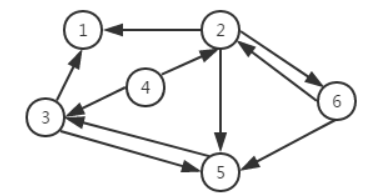
对于上图有向图,对应的顶点集合和边集合如下:
V(G)= {V1,V2,V3,V4,V5,V6}
E(G)= {<V2,V1>,<V3,V1>,<V4,V3>,<V4,V2>,<V3,V5>,<V5,V3>,<V2,V5>,<V6,V5>,<V2,V6>,<V6,V2>}
注意:
无向图也可以理解成一个特殊的有向图,就是边互相指向对方节点,A指向B,B又指向A。
3.混合图(mixed graph)
一个图结构中,边同时有的是有方向性有的是无方向型的图。在生活中混合图这种情况比较常见,比如城市道路中有些道路是单向通行,有的是双向通行。
** 4.顶点的度**
连接顶点的边的数量称为该顶点的度。顶点的度在有向图和无向图中具有不同的表示。对于无向图,一个顶点V的度比较简单,其是连接该顶点的边的数量,记为D(V)。 例如,上图所示的无向图中,顶点V5的度为3。而V6的度为2。
对于有向图要稍复杂些,根据连接顶点V的边的方向性,一个顶点的度有入度和出度之分。
入度是以该顶点为端点的入边数量, 记为ID(V)。
出度是以该顶点为端点的出边数量, 记为OD(V)。
这样,有向图中,一个顶点V的总度便是入度和出度之和,即D(V) = ID(V) + OD(V)。例如,上图所示的有向图中,顶点V5的入度为3,出度为1,因此,顶点V5的总度为4。
5.邻接顶点
邻接顶点是指图结构中一条边的两个顶点。 邻接顶点在有向图和无向图中具有不同的表示。对于无向图,邻接顶点比较简单。例如,在上图所示的无向图中,顶点V2和顶点V6互为邻接顶点,顶点V2和顶点V5互为邻接顶点等。
对于有向图要稍复杂些,根据连接顶点V的边的方向性,两个顶点分别称为起始顶点(起点或始点)和结束顶点(终点)。有向图的邻接顶点分为两类:
- 入边邻接顶点:连接该顶点的边中的起始顶点。例如,对于组成<V2,V6>这条边的两个顶点,V2是V6的入边邻接顶点。
- 出边邻接顶点:连接该顶点的边中的结束顶点。例如,对于组成<V2,V6>这条边的两个顶点,V6是V2的出边邻接顶点。
6.无向完全图
如果在一个无向图中, 每两个顶点之间都存在条边,那么这种图结构称为无向完全图。典型的无向完全图,如下图所示。
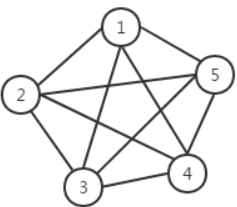
理论上可以证明,对于一个包含M个顶点的无向完全图,其总边数为M(M-1)/2。比如图四总边数就是5(5-1)/ 2 = 10。
7有向完全图
如果在一个有向图中,每两个顶点之间都存在方向相反的两条边,那么这种图结构称为有向完全图。典型的有向完全图,如下图所示。
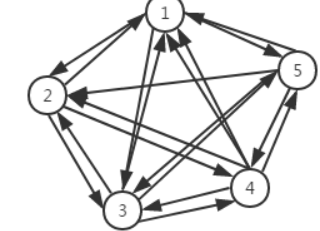
理论上可以证明,对于一个包含N的顶点的有向完全图,其总的边数为N(N-1)。这是无向完全图的两倍,这个也很好理解,因为每两个顶点之间需要两条边。
8.有向无环图(DAG图)
如果一个有向图无法从某个顶点出发经过若干条边回到该点,则这个图是一个有向无环图。有向无环图可以利用在区块链技术中。
9.无权图和有权图
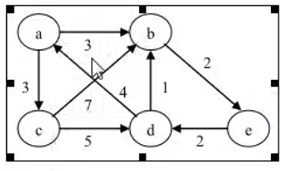
这里的权可以理解成一个数值,就是说节点与节点之间这个边是否有一个数值与它对应,对于无权图来说这个边不需要具体的值。对于有权图节点与节点之间的关系可能需要某个值来表示,比如这个数值能代表两个顶点间的距离,或者从一个顶点到另一个顶点的时间,所以这时候这个边的值就是代表着两个节点之间的关系,这种图被称为有权图
10.图的连通性
图的每个节点不一定每个节点都会被边连接起来,所以这就涉及到图的连通性,如下图:
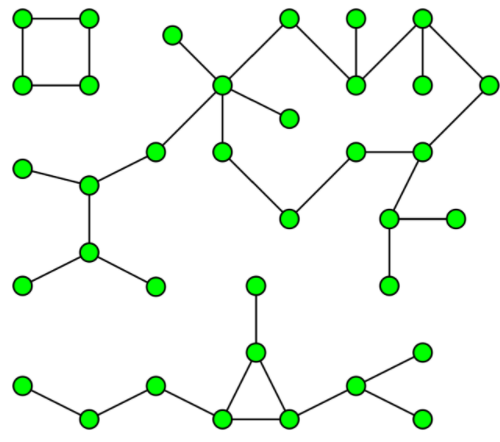
11.简单图 ( Simple Graph)
对于节点与节点之间存在两种边,这两种边相对比较特殊
1.自环边(self-loop):节点自身的边,自己指向自己。
2.平行边(parallel-edges):两个节点之间存在多个边相连接。
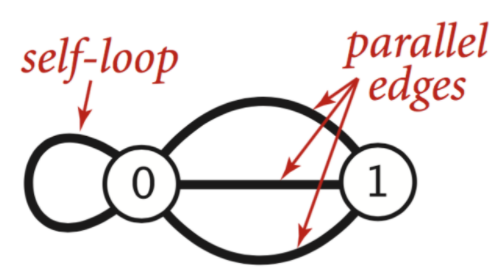
这两种边都是有意义的,比如从A城市到B城市可能不仅仅有一条路,比如有三条路,这样平行边就可以用到这种情况。不过这两种边在算法设计上会加大实现的难度。而简单图就是不考虑这两种边。
二 图的存储
1 链接矩阵: 二维数组 顺序表
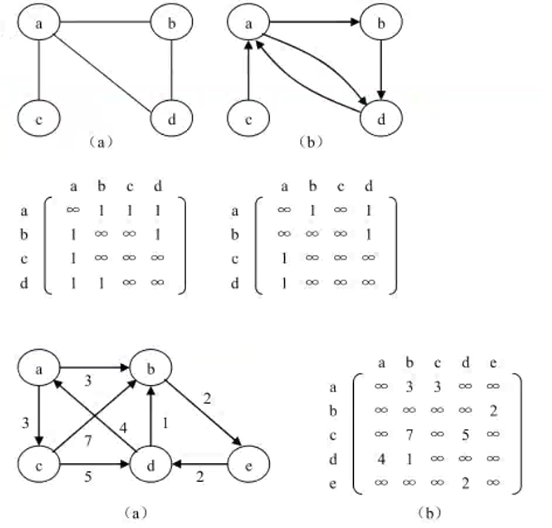
2 邻接表:链表
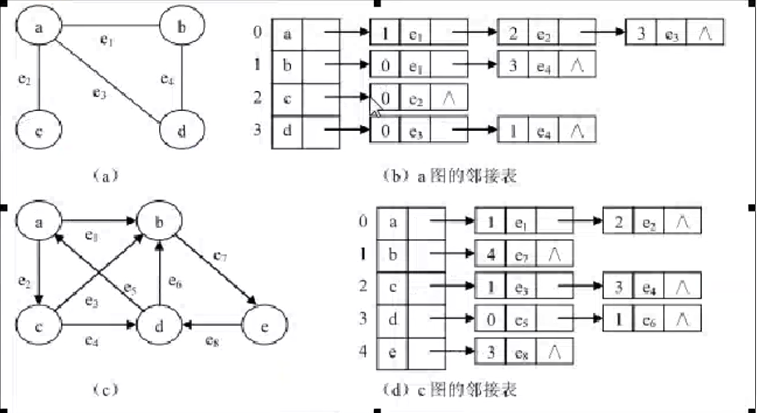
三 图的遍历
图的遍历就是从图中的某个节点出发,按某种方式对图中所有的顶点访问且仅访问一次,图的遍历是求解图的连通性,拓补排序,和关键路径等算法的基础
1:深度优先遍历(DFS)可递归可借助栈
类似于树的先序遍历,是树的先序遍历的推广
2:广度优先遍历(BFS) 借助度队列实现
类似于树的层次遍历,是树的层次遍历的推广
无向图遍历:
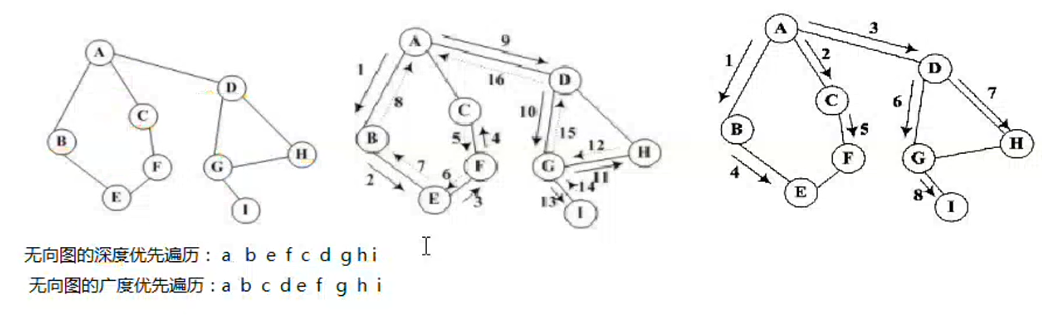
四 图的最短路径
在许多领域中,带权图都被用来描述某个网路,如通信,交通等,这种情况下每个边的权重就对应与两点之间的通信成本或交通费用,一类典型问题就是,在任意指定两点间若存在通路,那么最小的消耗是多少,这列问题实际就是带权图中两点之间最短路径的问题
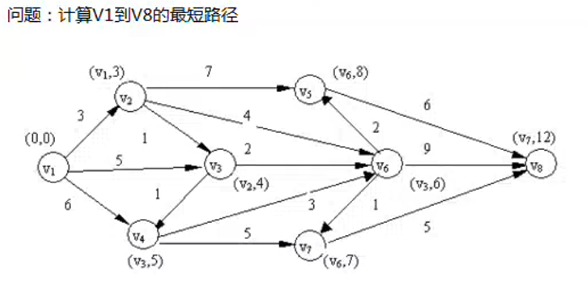
1 | 1: 段数最少的最短路径 |
迪克斯特拉算法解释:如求v1到v8的最短路径

五 实现
暂时没空,略